本章节讲解神经网络，组织结构如下：

Neural Networks: Learning
- Cost Function
- Backpropagation Algorithm
- Backpropagation Intuition
- Implementation Note Unrolling Parameters
- Gradient Checking
- Random Initialization
- Putting It Together
- Autonomous Driving

Cost Function

对于一个神经网络，我们用 $L$ 表示层数，用 $S_l$ 表示第 $l$ 层的神经元个数（不包含偏置）。然后我们分开讨论二元分类和多元分类。例如上图中， $L=4, s_1=3,s_2=s_3=5, s_4=4$ ，我们用 $s_L$ 表示最后一层的神经元个数。

二元分类： $S_L=1$
$K$ 元分类： $S_L=K$

然后我们回顾逻辑回归中的代价函数：

$J(\theta)=-\frac{1}{m}\left[\sum_{i=1}^{m} y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]+\frac{\lambda}{2 m} \sum_{j=1}^{n} \theta_{j}^{2}$

类似这个的话，我们对于 $K$ 元的分类问题就有这样的一个代价函数：

$J(\Theta)=-\frac{1}{m}\left[\sum_{i=1}^{m} \sum_{k=1}^{K} y_{k}^{(i)} \log \left(h_{\Theta}\left(x^{(i)}\right)\right)_{k}+\left(1-y_{k}^{(i)}\right) \log \left(1-\left(h_{\Theta}\left(x^{(i)}\right)\right)_{k}\right)\right]+\frac{\lambda}{2 m} \sum_{l=1}^{L-1} \sum_{i=1}^{s_{l}} \sum_{j=1}^{s_{l+1}}\left(\Theta_{j i}^{(l)}\right)^{2}$

其中， $h_{\Theta}(x) \in \mathbb{R}^{K} \quad\left(h_{\Theta}(x)\right)_{i}=i^{t h} \text { output }$ 。这个公式的原理和逻辑回归是大致类似的，唯一不同的是，对于每一行特征，我们都会给出 $K$ 个预测，基本上我们可以利用循环，对每一行特征都预测 $K$ 个不同结果，然后在利用循环在 $K$ 个预测中选择可能性最高的一个，将其与 $y$ 中的实际数据进行比较。

Backpropagation Algorithm

之前我们在计算神经网络预测结果的时候我们采用了一种正向传播方法，我们从第一层开始正向一层一层进行计算，直到最后一层的 $h_{\theta}\left(x\right)$ 。现在，为了计算代价函数的偏导数 $\frac{\partial}{\partial\Theta^{(l)}_{ij}}J\left(\Theta\right)$ ，所以我们需要通过最后一层的误差，一层一层反向求出各层的误差，举个例子神经网络如下，那么： $K=4，S_{L}=4，L=4$ 。

我们从最后一层的误差往前看：

我们用 $\delta_j^{(l)}$ 来表示第 $L$ 层的第 $j$ 个节点的误差，那么有对于最后一层，有 $\delta^{(4)}=a^{(4)}-y$ ，往前一层的话，就是 $\delta^{(3)}=\left({\Theta^{(3)}}\right)^{T}\delta^{(4)}\ast g’\left(z^{(3)}\right)$ ，其中 $g’(z^{(3)})$ 是 $S$ 形函数的导数，即 $g’(z^{(3)})=a^{(3)}\ast(1-a^{(3)})$ 。下一步是继续计算第二层的误差： $\delta^{(2)}=(\Theta^{(2)})^{T}\delta^{(3)}\ast g’(z^{(2)})$ 。因为第一层是输入变量，不存在误差。我们有了所有的误差的表达式后，便可以计算代价函数的偏导数了，假设 $λ=0$ ，即我们不做任何正则化处理时有： $\frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)=a_{j}^{(l)} \delta_{i}^{l+1}$ 。

重要的是清楚地知道上面式子中上下标的含义：

$l$ 代表目前所计算的是第几层。
$j$ 代表目前计算层中的激活单元的下标，也将是下一层的第 $j$ 个输入变量的下标。
$i$ 代表下一层中误差单元的下标，是受到权重矩阵中第 $i$ 行影响的下一层中的误差单元的下标。

如果我们考虑正则化处理，并且我们的训练集是一个特征矩阵而非向量。在上面的特殊情况中，我们需要计算每一层的误差单元来计算代价函数的偏导数。在更为一般的情况中，我们同样需要计算每一层的误差单元，但是我们需要为整个训练集计算误差单元，此时的误差单元也是一个矩阵，我们用 $\Delta^{(l)}_{ij}$ 来表示这个误差矩阵。第 $l$ 层的第 $i$ 个激活单元受到第 $j$ 个参数影响而导致的误差。

总的来说，就是先算出 $\triangle$ ，再算出 $D$ ，然后我们就可以根据 $D$ 算出偏导了。即：

$\frac{\partial}{\partial \Theta_{i j}^{(l)}} J(\Theta)=D_{i j}^{(l)}$

Backpropagation Intuition

上一小节介绍了什么是反向传播算法，相对于线性回归和逻辑回归而言，这确实较为复杂了。这一小节，深入讨论一下反向传播算法的步骤。假如有这么一个网络：

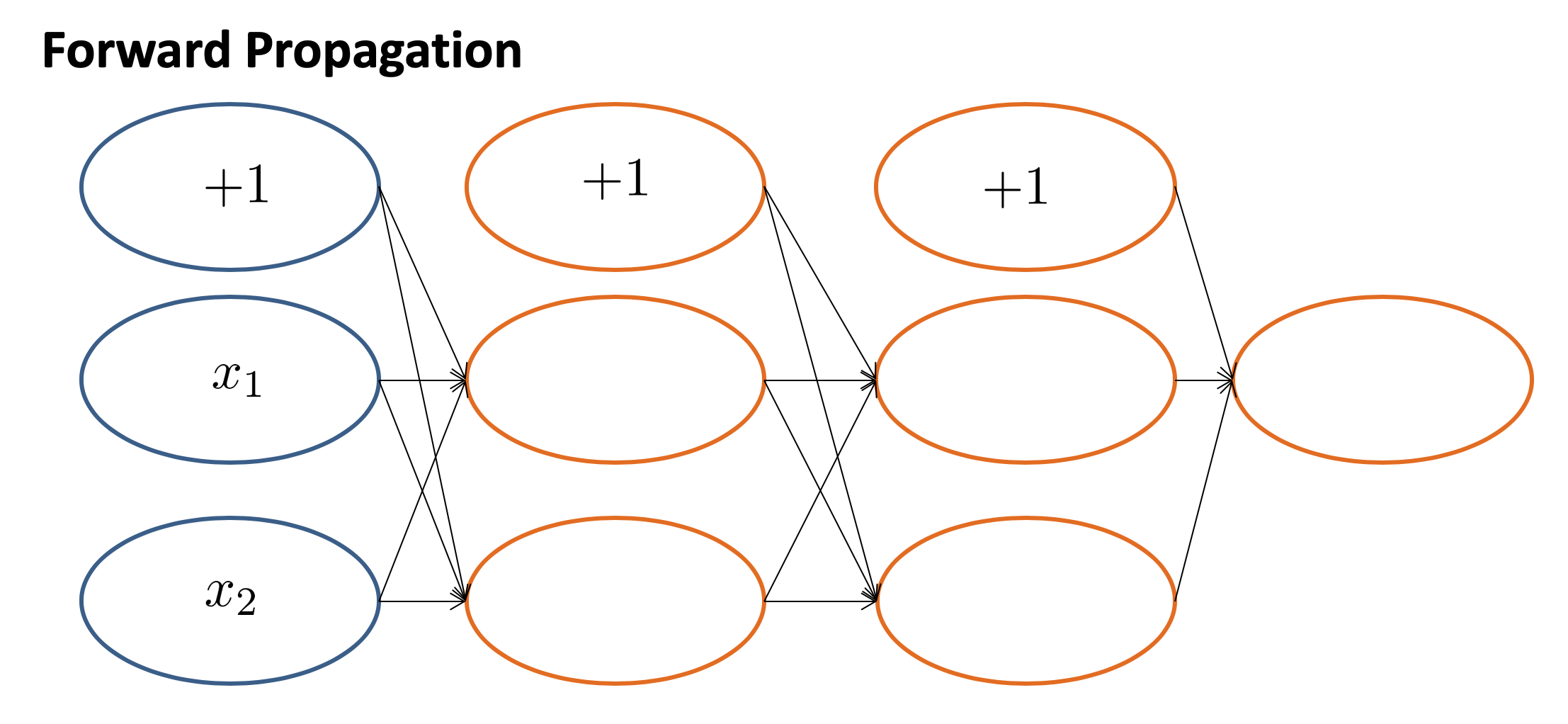
对于一个输入 $(x^{(i)},y^{(i)})$ ，我们填入中间的计算过程，为：

$\delta^{(l)}_{j}$ 相当于是第 $l$ 层的第 $j$ 单元中得到的激活项的“误差”，即”正确“的 $a^{(l)}_{j}$ 与计算得到的 $a^{(l)}_{j}$ 的差，而 $a^{(l)}_{j}=g(z^{(l)})$ ，（g为sigmoid函数）。我们可以想象 $\delta^{(l)}_{j}$ 为函数求导时迈出的那一丁点微分，所以更准确的说 $\delta^{(l)}_{j}=\frac{\partial}{\partial z^{(l)}_{j}}cost(i)$ 。

Implementation Note Unrolling Parameters

这一节讲的实现过程中多个特征矩阵如何用一个矩阵表示，忽略。

Gradient Checking

当我们对一个较为复杂的模型（例如神经网络）使用梯度下降算法时，可能会存在一些不容易察觉的错误，意味着，虽然代价看上去在不断减小，但最终的结果可能并不是最优解。

为了避免这样的问题，我们采取一种叫做梯度的数值检验（Numerical Gradient Checking）方法。这种方法的思想是通过估计梯度值来检验我们计算的导数值是否真的是我们要求的。

对梯度的估计采用的方法是在代价函数上沿着切线的方向选择离两个非常近的点然后计算两个点的平均值用以估计梯度。即对于某个特定的 $\theta$ ，我们计算出在 $\theta$ - $\varepsilon$ 处和 $\theta$ + $\varepsilon$ 的代价值（ $\varepsilon$ 是一个非常小的值，通常选取 0.001），然后求两个代价的平均，用以估计在 $\theta$ 处的代价值。

当 $\theta$ 是一个向量时，我们则需要对偏导数进行检验。因为代价函数的偏导数检验只针对一个参数的改变进行检验，下面是一个只针对 $\theta_1$ 进行检验的示例：

$\frac{\partial}{\partial\theta_1}=\frac{J\left(\theta_1+\varepsilon_1,\theta_2,\theta_3...\theta_n \right)-J \left( \theta_1-\varepsilon_1,\theta_2,\theta_3...\theta_n \right)}{2\varepsilon}$

最后我们还需要对通过反向传播方法计算出的偏导数进行检验。

根据上面的算法，计算出的偏导数存储在矩阵 $D_{ij}^{(l)}$ 中。检验时，我们要将该矩阵展开成为向量，同时我们也将 $\theta$ 矩阵展开为向量，我们针对每一个 $\theta$ 都计算一个近似的梯度值，将这些值存储于一个近似梯度矩阵中，最终将得出的这个矩阵同 $D_{ij}^{(l)}$ 进行比较。

Random Initialization

任何优化算法都需要一些初始的参数。到目前为止我们都是初始所有参数为0，这样的初始方法对于逻辑回归来说是可行的，但是对于神经网络来说是不可行的。如果我们令所有的初始参数都为0，这将意味着我们第二层的所有激活单元都会有相同的值。同理，如果我们初始所有的参数都为一个非0的数，结果也是一样的。

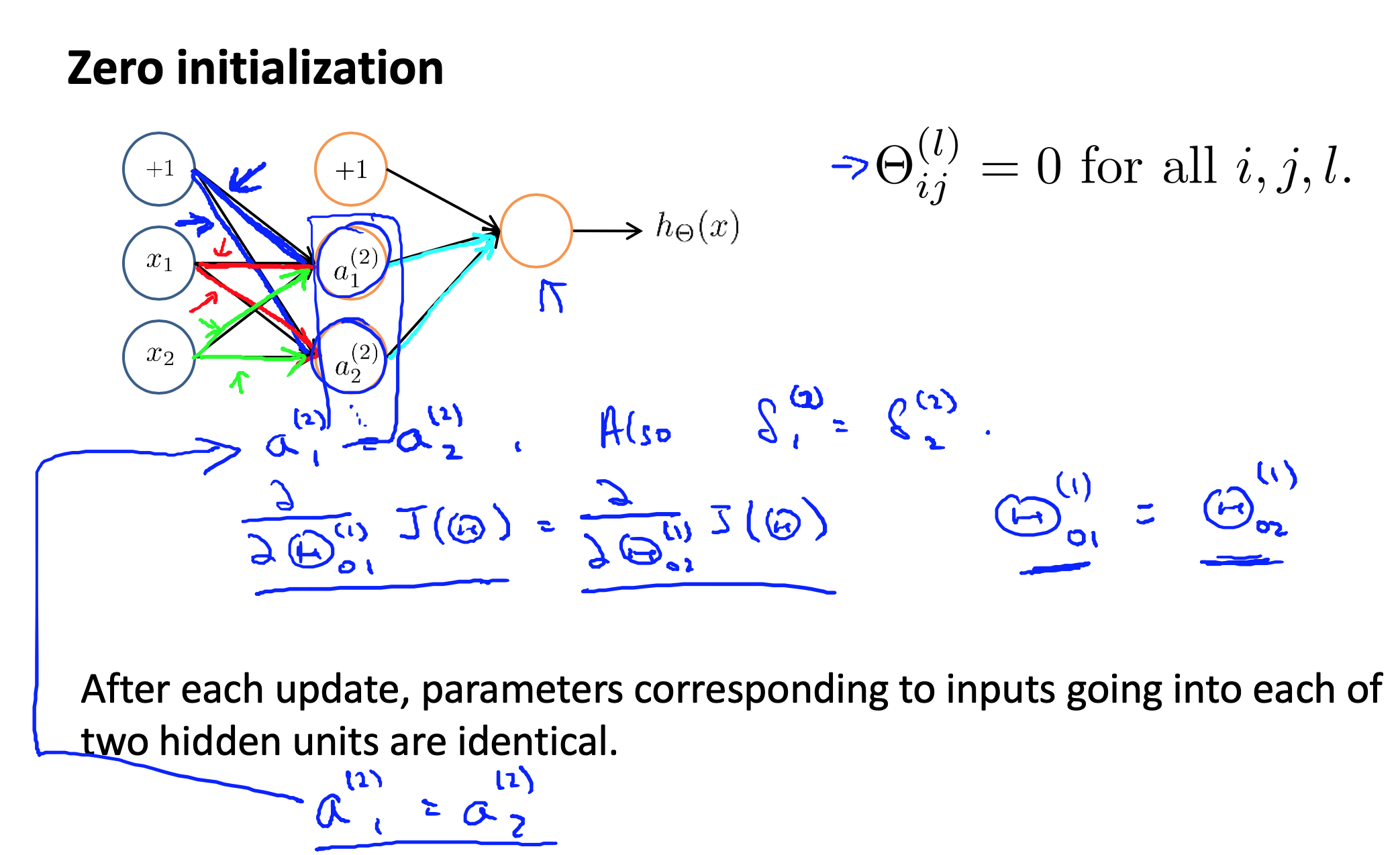
Putting It Together

小结一下使用神经网络时的步骤：

网络结构：第一件要做的事是选择网络结构，即决定选择多少层以及决定每层分别有多少个单元。第一层的单元数即我们训练集的特征数量。最后一层的单元数是我们训练集的结果的类的数量。如果隐藏层数大于1，确保每个隐藏层的单元个数相同，通常情况下隐藏层单元的个数越多越好。我们真正要决定的是隐藏层的层数和每个中间层的单元数。

训练神经网络：

参数的随机初始化
利用正向传播方法计算所有的 $h_{\theta}(x)$
编写计算代价函数 $J$ 的代码
利用反向传播方法计算所有偏导数
利用数值检验方法检验这些偏导数
使用优化算法来最小化代价函数

Autonomous Driving

讲了一个应用案例，略。